关键点论文详解之:Human Pose Regression with Residual Log-likelihood Estimation(RLE)
小小小绿叶
于 2022-08-24 19:02:29 发布
28
收藏
分类专栏: 关键点估计 文章标签: 机器学习 人工智能 深度学习
版权
关键点估计
专栏收录该内容
4 篇文章0 订阅
订阅专栏
最近看了一篇论文Human Pose Regression with Residual Log-likelihood Estimation(RLE)很有意思,而且效果贼棒,与大家分享一下。
前言
做过关键点的同学都知道,一般Heatmap-based方法在性能上会优于Regression-based的方法。因为Heatmap-based方法通过显式地渲染高斯热图,让模型学习输出的目标分布,将输入图片滤波成为最终希望得到的高斯热图即可,这极大地简化了模型的学习难度,并且这种方式规定了学习的分布,相对于除了结果以外内部一切都是黑盒的Regression-based方法,对于各种情况(遮挡、动态模糊、截断等)要鲁棒得多。
但是,相较于Heatmap-based方法,Regression-based也有其无法比拟的地方。Regression-based方法不需要生成heatmap,计算成本内存开销较低。同时,Regression-based方法输出是连续的,不必担心量化误差。如果,Regression-based能够拥有Heatmap-based的精度,那么,对于项目落地来说,简直是如虎添翼。
动机
论文发现在Regression-based方法中,使用L1 loss效果优于L2 loss。从极大似然估计的角度来理解,L1 loss服从拉普拉斯的先验假设,而L2 loss则服从高斯分布先验假设。假设网络能够学习到真实误差的概率分布,这样的无监督信息对于regression回归是非常有益的。
P Θ ( X ∣ I ) P_\Theta{(X|\mathcal{I})}P
Θ
(X∣I),表示GT出现在位置x中的概率,其中Θ表示可学习的模型参数,μ g \mu_gμ
g
表示GT坐标。-log就是它的极大似然估计。在这个公式中,不同的回归损失本质上是不同的输出概率分布的假设。假设概率密度函数是高斯分布,那么模型需要预测两个值μ ^ , σ ^ \hat{\mu},\hat{\sigma}
μ
^
,
σ
^
来构建P Θ ( X ∣ I ) P_\Theta{(X|\mathcal{I})}P
Θ
(X∣I)。
当我们最大化它的似然函数,那么损失函数就可以看作公式2。如果,我们把公式2中的σ ^ \hat{\sigma}
σ
^
看作常数,损失就退化成标准的L2 loss:L = ( μ g − μ ^ ) 2 L=(\mu_g-\hat{\mu})^2L=(μ
g
−
μ
^
)
2
.同理,当假设概率密度函数是拉普拉斯分布时,损失退化成标准的L1 loss。
为了获得真实的误差概率分布,论文使用Flow-based generative model去模拟并生成误差概率分布。
Flow-based generative model
论文使用Flow-based方法生成误差概率分布,想详细了解Flow-based generative model的请参考这里。下面我简单介绍一下这部分内容。
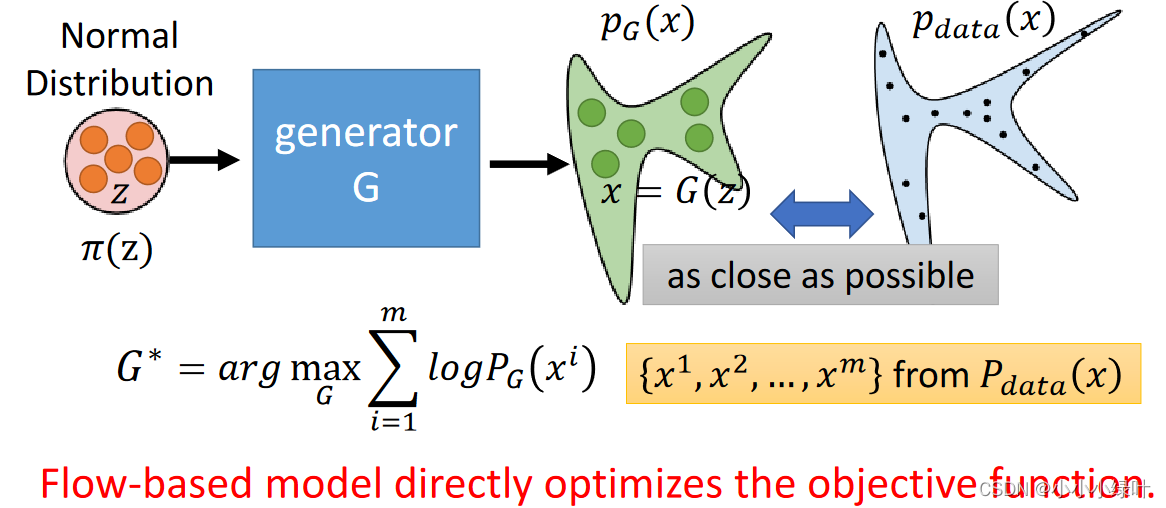
假设我们已知两个概率密度函数π ( z ) , p ( x ) \pi(z),p(x)π(z),p(x),这两个概率密度函数存在x = f ( z ) x=f(z)x=f(z)这样的变化关系。根据两个函数对应部分积分的面积相等,我们可以获得p ( x ) ∣ d e t ( J f ) ∣ = π ( z ) p(x)|det(J_f)|=\pi(z)p(x)∣det(J
f
)∣=π(z)等式。下图中的P G P_GP
G
就是一个随机参数的概率密度函数,我们从P d a t a P_{data}P
data
真实样本分布中抽取样本x i x^ix
i
,将其带入P G ( x i ) P_G(x^i)P
G
(x
i
),并max(l o g P G ( x i ) logP_G(x^i)logP
G
(x
i
)),通过不断迭代就可以使P G P_GP
G
越来越接近P d a t a P_{data}P
data
。
Design
下面介绍论文是如何设计Flow-based model,获取生成器的极大似然损失,从而生成真实误差概率分布,提高Regression-based精度。
1.Basic Design
假设基础分布P Θ ( Z ∣ I ) P_\Theta(Z|I)P
Θ
(Z∣I)服从高斯分布,参数μ , σ \mu,\sigmaμ,σ来自regression的predict(这里会多预测2个值,作为σ \sigmaσ),同时X = f ϕ ( z ) X=f_\phi(z)X=f
ϕ
(z),其中ϕ \phiϕ是flow model的可学习参数。那么P Θ P_\ThetaP
Θ
如公式3所示。
直接学习关键点真实坐标μ g \mu_gμ
g
的样本分布,训练时从真实样本即GT:μ g \mu_gμ
g
中抽样,通过最大化L m l e L_{mle}L
mle
,将P Θ , P d a t a P_\Theta,P_{data}P
Θ
,P
data
拉近。
公式4中的loss会引导ϕ \phiϕ学习拟合所有图像中µg的分布。然而,我们想要了解的分布是关于输出如何偏离输入图像上的GT,而不是GT本身在所有图像中的分布。
2.Reparameterization
学习误差概率分布,用重参数化技巧实现Basic Design的目标。基础分布π ( z ˉ ) \pi(\bar{z})π(
z
ˉ
)设置为标准正态分布,X ˉ = f ϕ ( z ) \bar{X}=f_\phi(z)
X
ˉ
=f
ϕ
(z).L m l e L_{mle}L
mle
如下所示,其中误差μ ˉ g = ( μ g − μ ^ ) / σ ^ \bar{\mu}_g=(\mu_g-\hat{\mu})/\hat{\sigma}
μ
ˉ
g
=(μ
g
−
μ
^
)/
σ
^
。
由于训练过程中regression预测的μ ^ \hat{\mu}
μ
^
与f ϕ f_\phif
ϕ
是耦合的,在训练的开始阶段,分布的形状还不靠谱,这增加了训练回归模型的难度,并可能会降低模型的性能。
3.Residual Log-likelihood Estimation.
为了便于训练,论文开发了一个残差对数似然结构来减少这两个模型之间的依赖性。
形式上,流模型预测的分布P ϕ ( X ˉ ) P_\phi(\bar{X})P
ϕ
(
X
ˉ
)试图拟合最优的潜在分布P o p t ( X ˉ ) P_{opt}(\bar{X})P
opt
(
X
ˉ
),如公式6被分成3部分,其中Q ( X ˉ ) Q(\bar{X})Q(
X
ˉ
)服从(0,1)正态分布,l o g P o p t ( X ˉ ) s ∗ Q ( X ˉ ) log\frac{P_{opt}(\bar{X})}{s*Q(\bar{X})}log
s∗Q(
X
ˉ
)
P
opt
(
X
ˉ
)
是论文提出的残差对数似然结构。s是为了确保残差对数似然结构满足概率密度函数的要求。论文假设Q ( X ˉ ) Q(\bar{X})Q(
X
ˉ
)大概匹配误差潜在分布,l o g P o p t ( X ˉ ) s ∗ Q ( X ˉ ) log\frac{P_{opt}(\bar{X})}{s*Q(\bar{X})}log
s∗Q(
X
ˉ
)
P
opt
(
X
ˉ
)
能够补足Q ( X ˉ ) Q(\bar{X})Q(
X
ˉ
)与误差潜在分布的不同。最终的loss如公式8所示,其中s对结果影响不大。